By Foroohar Foroozan, signal processing scientist, Analog Devices
Imagine a world where the word “hospital” is unheard of! This could be reality in a few decades’ time, when all health information will be recorded and monitored remotely via sensors. Homes will be equipped with various sensors to measure air quality, temperature, noise, light and air pressure, and, based on the home owners’ health information, systems will be adjusted to optimise their wellbeing.
As expected, heart rate (HR) monitoring will be a key parameter for those systems, and it is already found in many existing wearable devices. These devices measure photoplethysmography (PPG) signals, obtained by illuminating the human skin using LEDs, then photodiodes measure intensity changes of the blood flow using the reflected light.
The PPG signal morphology is like the arterial blood pressure (ABP) waveform, making it a signal of choice within the scientific community as a non-invasive HR monitoring tool. The periodicity of the PPG signal corresponds to the cardiac rhythm, helping estimate HR. However, this estimation can be degraded by poor blood perfusion, ambient light and, most significantly, motion artifacts (MA).
Many signal-processing techniques have been proposed to remove MA noise, which includes ADI’s motion-rejection and frequency-tracking algorithm, by using a three-axis acceleration sensor close to the PPG sensor.
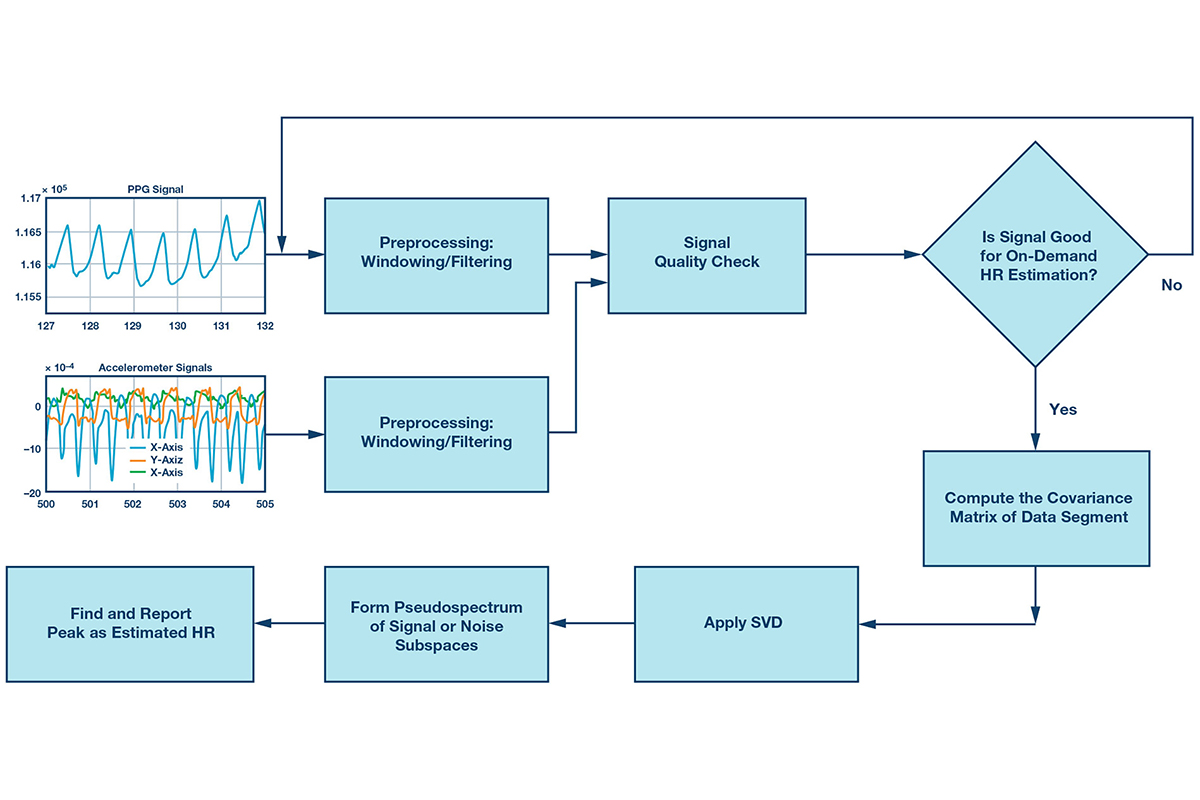
This article focuses on adapting the multiple signal classification (MuSiC) frequency estimation algorithm for high precision, on-demand HR estimation with PPG signals from the wrist, using ADI’s healthcare watch platform; see Figure 1.

PPG Signals
As light is emitted by an LED, blood levels and tissues absorb various amounts of photons, varying the readout of the photodetector. As the photodetector measures the variations in blood pulsations, it outputs a current that’s amplified and filtered for further analysis.
Figure 2a shows a general PPG signal consisting of AC and DC components. The DC component detects the optical signal reflected from tissue, bone and muscle, and the average blood volume of both arterial and venous blood. On the other hand, the AC component indicates changes in blood volume that occur between the systolic and diastolic phases of the cardiac cycle, where the fundamental frequency of the AC component depends on the HR.
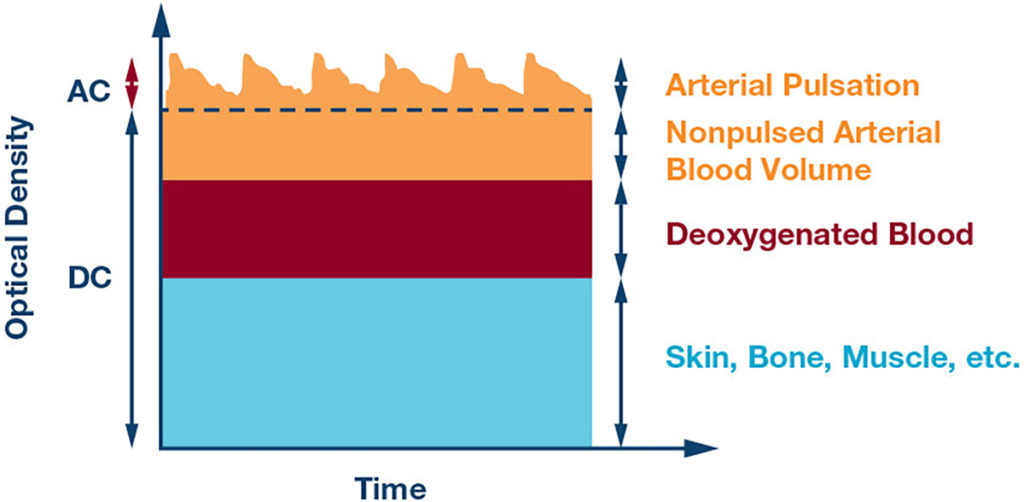
Figure 2b shows the PPG signal from the ADI ADPD107 multisensory watch, which measures multiple vital signs on the human wrist, including an electrocardiogram (ECG), electrodermal activity (EDA), accelerometer (ACC) and temperature sensors.

There are similarities between the PPG and ABP waveforms; the ABP waveform is created by blood being pumped out of the left ventricle. The main pressure travels down the systemic vascular network and reaches several sites, causing reflection due to significant changes in arterial resistance and compliance. The first site is the juncture between the thoracic and abdominal aorta, creating the first reflection, commonly known as the late systolic wave.
The second reflection site is the juncture between the abdominal aorta and common iliac arteries. The main wave is reflected again, which makes a small dip, called the dicrotic notch, observable between the first and second reflections. There are other additional minor reflections, which are smoothed in the PPG signals.
Preprocessing of PPG Signals
There’s a susceptibility of the PPG signal to poor blood perfusion of the peripheral tissues and motion artifact. To minimise the influence of these factors in subsequent phases of the PPG analysis for HR estimation, a preprocessing stage is required. A bandpass filter is needed to remove both high frequency components (such as power sources) of the PPG signals, and low frequency components, such as changes in capillary density, venous blood volume, temperature variations.
Figure 3a shows a PPG signal after filtering. A set of signal quality metrics is used to find the first window suitable for the on-demand algorithm. The first check involves ACC data and the PPG signal to determine whether a segment of motion-free data can be detected, followed by measurement of the other signal quality metrics. Estimates from such a window of data are rejected by the on-demand algorithm if there is motion above a certain threshold of the absolute values of the ACC data in three directions.

The next signal quality check is based on certain autocorrelation having features of the data segment. One example of the autocorrelation of the filtered PPG signal is shown in Figure 3b.

Autocorrelation of acceptable signal segments exhibits properties with at least one local peak and not more than a certain number of peaks corresponding to the highest possible HR, having the local peaks in a descending order with increasing lags, and a few others.
Autocorrelation is only computed for lags that correspond to meaningful heart rates within a range, from 30bpm to 220bpm.
When enough data segments pass the quality checks consecutively, the second stage of the algorithm extracts the accurate HR using the MuSiC-based algorithm.
On-Demand HR Estimation
MuSiC is a subspace-based method that uses a model of harmonic signals to estimate frequency with high precision. When it comes to the PPG signals corrupted with noise, the Fourier Transform (FT) approach may not do well, since we are seeking a high-resolution HR estimation algorithm. Also, FT distributes time-domain noise uniformly throughout the frequency domain, limiting the certainty of estimation, so it is difficult to observe a small peak near a large peak using FT. Therefore, in this study, we used the MuSiC-based algorithm for HR frequency estimation.
The key idea behind MuSiC is that the noise subspace is orthogonal to the signal subspace, so zeroes of the noise subspace will indicate signal frequencies. The following steps show a summary of this algorithm used for HR estimation:
- Remove the mean and linear trend from the data;
- Compute the data’s covariance matrix;
- Apply singular value decomposition (SVD) to the covariance matrix;
- Compute the signal subspace order;
- Form the pseudospectrum of the signal or noise subspaces;
- Find the peaks of the MuSiC pseudospectrum, and use them as the HR estimate.
MuSiC applies a singular value decomposition and searches spectral peaks in the full range of frequencies.
Assume a window of length m of the filtered PPG signal, denoted as xm and m ≤ L (L is the total samples of the filtered PPG signal in a given window). The first step is to form the sample covariance matrix:
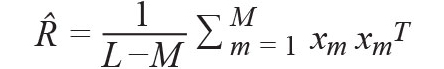
Then, an SVD is applied to the sample covariance matrix:

where U is the left eigenvectors, Λ is the diagonal matrix of the eigenvalues and V is the right eigenvectors of the covariance matrix. The subscripts s and n stand for the signal and noise subspaces.
As mentioned earlier, the MuSiC-based algorithm is modified for HR estimation using prior knowledge that the signal has passed the quality checking stage, so that the only frequency content in the signal after the preprocessing step is the HR frequency.
Next, we form the signal and noise subspaces, assuming the model order only contains a single tone, as follows:
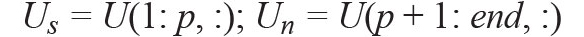
where p = 2 is the model number. Only frequencies within the meaningful HR limits are considered here, which significantly reduces computations and makes a real-time implementation for embedded algorithms feasible.
The search frequency vector is defined as:

where k is the frequency bin within the frequency range of interest for HR, and L is window length for the data in xm(t). Then, the following psesudospectrum takes the noise subspace eigenvectors to find the peaks of the MuSiC:

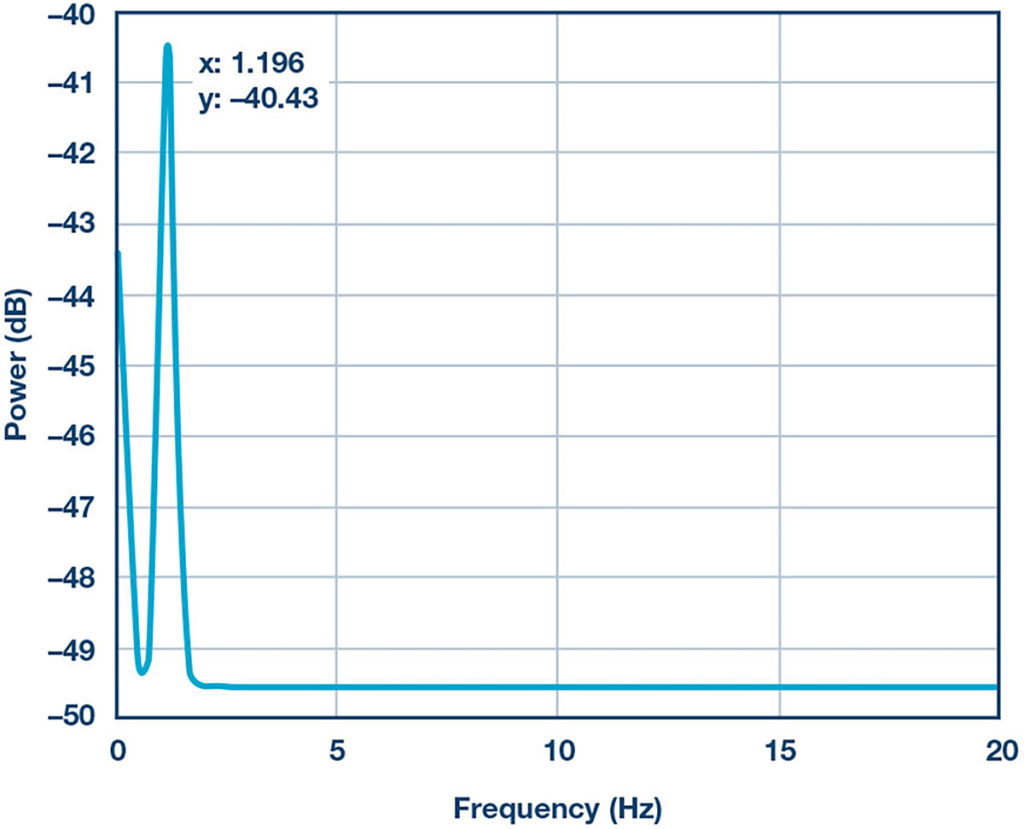
The word psesudospectrum is used here because it indicates the presence of sinusoidal components in the studied signal, but it is not a true power spectral density. One sample result of the MuSiC-based algorithm on a five-second window of data is given in Figure 4, which shows a sharp peak at 1.96Hz, translating to HR of 117.6bmp.
HR Estimation Results
The performance of this algorithm was tested on a dataset comprising 1289 cases (data1), where at first the test subjects were asked to stand at rest. Table 1 shows the results of the MuSiC-based algorithm and indicates whether the estimated HR is within 2bpm and 5bpm of the reference (ECG), as well as the 50th percentile (median) and 75th percentile of the estimation times.
| Metric | 2 bpm Accuracy | 5 bpm Accuracy | 50th Percentile | 75th Percentile |
| Accuracy (data1) | 93.7% | 95.2% | 5.00 sec | 5.00 sec |
| Accuracy (data2) | 93.4% | 94.1% | 5.00 sec | 5.00 sec |
The second row of Table 1 shows the performance of the algorithm when there is a periodic motion (such as walking, jogging, running) over a dataset of 298 test cases (data2). The algorithm is successful if either the data is rejected as unreliable by sensing a motion or by accurately estimating the HR despite a motion. In terms of memory usage, assuming a buffer size of 500 (that is 5s at 100Hz), the total memory needed is around 3.4kB with 2.83 cycle per call for the frequency range of interest (30-220bpm).